跨境从业用到过的知识
1,最最基础的原理
1.1 基础知识幂函数的应用
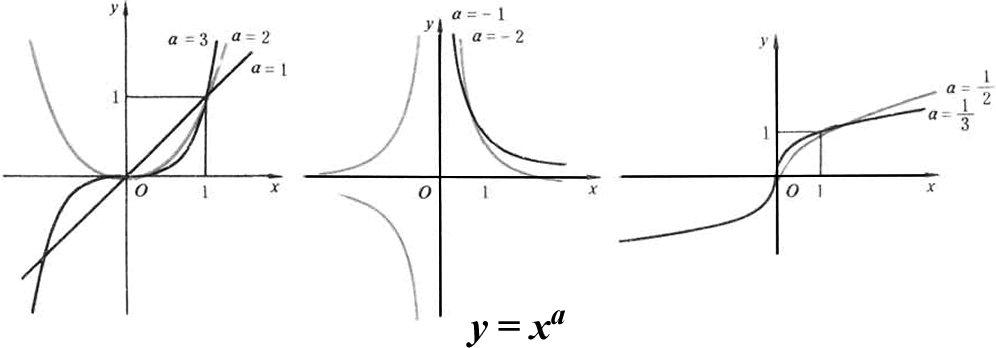
自变量 x 在底数的位置上,y=x^a(a 不等于 1). a 不等于 1,但可正可负,取不同的值,图像及性质是不一样的。
高中数学里面,幂函数主要要掌握 a=-1、2、3、1/2 时的图像即可。其中当 a=2 时, 函数是过原点的二次函数。 其他 a 值的图像可自己通过描点法画下并了解下基本图像的走向即可。
性质: 根据图象,幂函数性质归纳如下:
(1)所有的幂函数在(0,+∞)都有定义,并且图象都过点 (1,1); (2)当 a>0 时,幂函数的图象通过原点,并且在区间[0,+ ∞)上是增函数. 特别地,当 a>1 时,幂函数的图象下凸;当 0<a<1 时,幂函数的图象上凸;
(3)当 a<0 时,幂函数的图象在区间(0,+∞)上是减函数.在第一象限内, 当 x 从右边趋向原点时,图象在 y 轴右方无限地逼近 y 轴正半轴,当 x 趋 于+∞时,图象在轴 x 上方无限地逼近轴 x 正半轴。 指出:此时 y=x0=1;定义域为(-∞,0)∪(0,+∞),特别强调, 当 x 为任何非零实数时,函数的值均为 1,图像是从点(0,1)出发,平行于 x 轴的两条射线,但点(0,1)要除外。
1.2 相关应用-长尾分布

A long tail distribution has tails that taper off gradually rather than drop off sharply. They are a subset of heavy-tailed distributions. It’s easy to visualize the idea of a long tailed function, and slightly harder to make it concrete.
If we want to be rigorous, though, there is a exact mathematical definition of a long tailed function (Foss et. al, 2013):
(ultimately positive) function f is defined according to a limit —a term introduced in calculus. Very basically, the limit tells you where the distribution converges to at a certain point. In this case, if the ratio of x + y and x converge to 1 as the x-values get much larger, then the distribution is long-tailed:
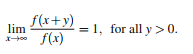
e long tailed property of distributions carries over into many derivative distributions.
If f1, f2… fn are all long tailed, then:
Any distribution that can be expressed as a product of these, fx= f1 · f2… · fn is also long tailed.
Any distribution that can be expressed as a linear combination of these is long tailed. That means that any function
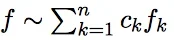
Commerce and marketing schemes often find that there sales can best be modeled by long tail distributions. For instance, an internet store may have certain items with very high sales (modeled by the center of the distribution curve) and a large number of items with much lower sales (modeled by the long tail).
Although the sales volume for every individual item in the tail may be negligible, there are enough items that they play a significant role in the general profit taking. In fact, the profit from low-sale volume items can rival or even sometimes leave in the dust the profit made from best-sellers—provided only the tail is long enough.
1.3长尾分布应用在电商平台
1.3.1 亚马逊平台
对于大部分的行业软件,如卖家精灵,数派,基本上是根据反比例函数结合机器学习来根据Bsr 排名的权重来反推销量。
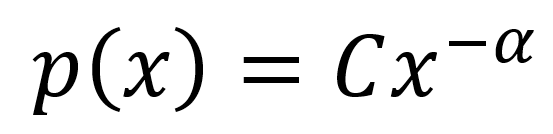
To people that don’t understand them, they manifest as ‘unfairness’, which they are. Unlike normal distributions, long tailed phenomena do not centre around a mid-point. They’re totally unsymmetrical and extreme events are rare, unpredictable but have gargantuan impacts when they eventually occur.
There are two models that we can use to map-out how these long-tailed distributions occur.
Preferential attachment: Imagine a network consisting of nodes and connections between nodes. The more connected a node is, the more likely it is to receive new links [3].
Preferential attachment often plays out in social domains. Looking at Instagram as an example, if you think about accounts as nodes and followers as connections; the more followers an account has, the more likely it is to receive more followers. The distribution of followers across social media accounts is a likely long tailed.
Self-organized Criticality: Imagine an empty N by N grid. A random site on the grid is chosen, if empty the site grows a tree with a probability g. If a site contains a tree lightening hits the site with a probability of (1-g). The lightening struck tree catches fire and the fire spreads to all connected trees[1].
In plain English, most forest fires are small but there exists a point where the forest becomes so dense that a fire could be gigantic.
Here’s a cool simulation of self-organized criticality playing out in the forest fire model.
Taking earthquakes as an example of a phenomenon that roughly follows a power law distribution with an exponent of 2[1].
An earthquake of magnitude 9 would be the size of the 2011 earthquake in Honshu Japan. It was estimated to have killed around 29,000 people and damaged nuclear reactors [5]. According to our assumptions about the distribution of earthquakes, an earthquake of this magnitude occurs with a probability of around one-in-a-million each day. Across 1 century this one in a million event has a probability of occurrence of around 3.5%.
Given the devastation that it could cause, suddenly this seems very concerning. It becomes even more so when you realise that the most earthquakes are between 5–5.9 on the Richter scale [6], a-thousand to ten-thousand times weaker than our one-in-a-million event.
Lack of awareness of long tailed phenomena will cause governments to be ill-prepared for these extreme events leading to mass destruction.
在亚马逊提供给我们的ABA数据中,也是可以根据ABA的排名进行搜索量反推的
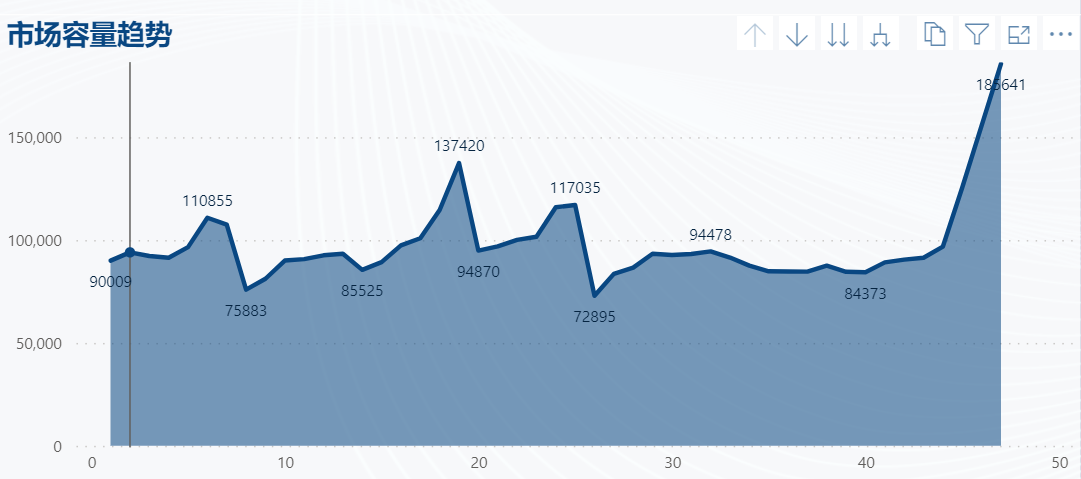
利用ABA数据反推市场容量就是利用这样的逻辑,从数据类型说,我们把定序尺度转化成了定比尺度。
1.3.2 二项分布在广告的应用基础知识
对于离散随机变量,有一个最重要的概率分布,它是 二项分布 (binomial distribution) 。二项分布处于二元数据。因为二元数据的情况非常多,所以二项分布使用频繁。
二项分布的三个要素。首先,试验现象有两种结果,并且成功概率是常量。这种实验被称为 伯努利试验验 (Bernoulli trial) 。其次,你观察试验结果 n 次。第三,你对成功的结果计数,记为 x 。这三个元素被结合成一个公式,它给���了在 n 次试验中取得特定数量成功结果的概率。公式如下:
$$
P (x) = \frac {n!}{x!(n - x)!} p^x (1 - p)^{n-x}, x = 0,1,2,…,n
$$
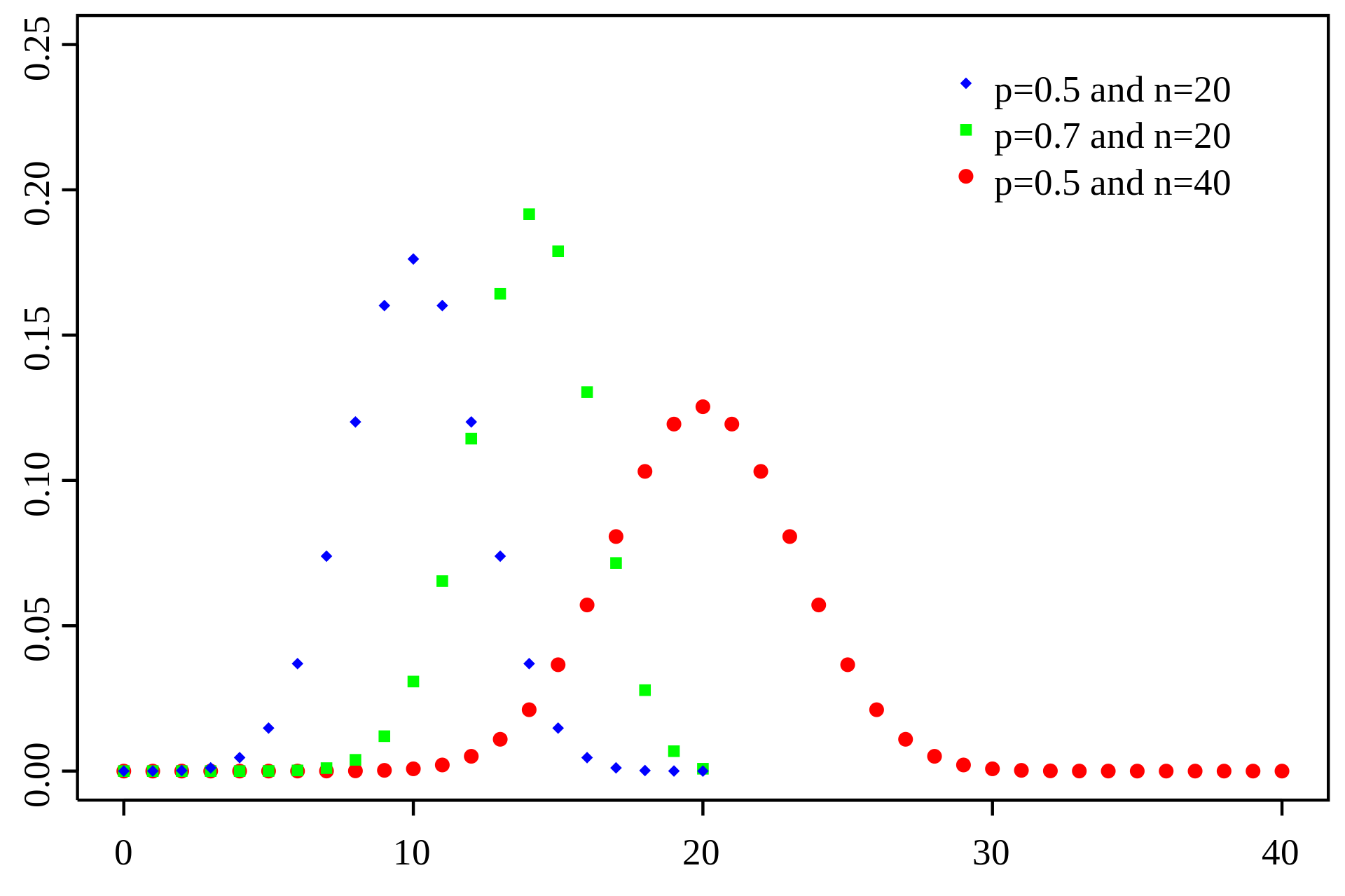
概率质量函数
累积分布函数
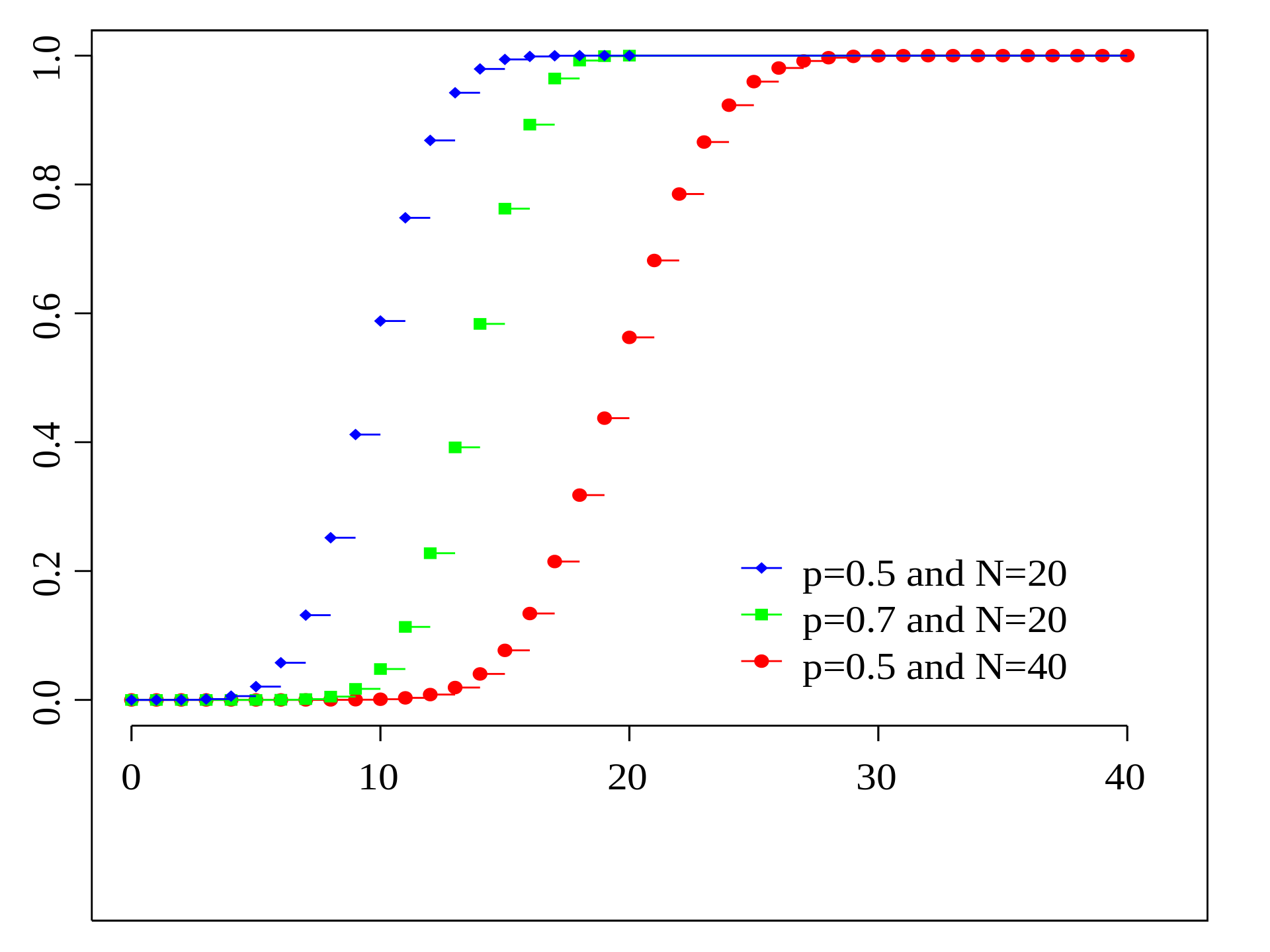
- 二项分布是一个离散概率分布,用于只有两个独立互斥结果的随机变量 —— 成功或者失败。它给出了对于随机变量的 n 个结果,其中 x 个成功的概率。也叫做试验成功的概率。
- 二项分布假定所有试验的概率 p 都是固定的,它的均值等于 n 乘以 p ,标准差等于 n 乘以 p 乘以 (1 - p),然后求平方根。
- 二项分布根据 p 的变化可以向右或者向左偏斜,或者对称。当 p 接近 0 时是右偏态,当 p 接近 1 时是左偏态。二项分布公式如下:
$$
P (x) = \frac {n!}{x!(n - x)!} p^x (1 - p)^{n-x}, x = 0,1,2,…,n
$$
速记为 X∼B(N,P)
- 二项分布的累积概率分布公式如下:
$$
F (x) = P (X \leq x) = \sum_{k = 0}^{x} \frac {n!}{k!(n - k)!} p^k (1 - p)^{n - k}
$$
1.3.3 对广告点击和转化的运用
为了解释这个问题,我们依然要接受一个和现实不会完全相符的假设,即:一个产品的转化率不会因为客户的不同和时间的不同而发生变化。
对于产品转化率为10%的一个关键词,意味着每一次点击的并且出单的概率是10%,不出单的概率的90%。
在这样的假设下,广告的点击出单概率即转化率可以近似看成二项分布。
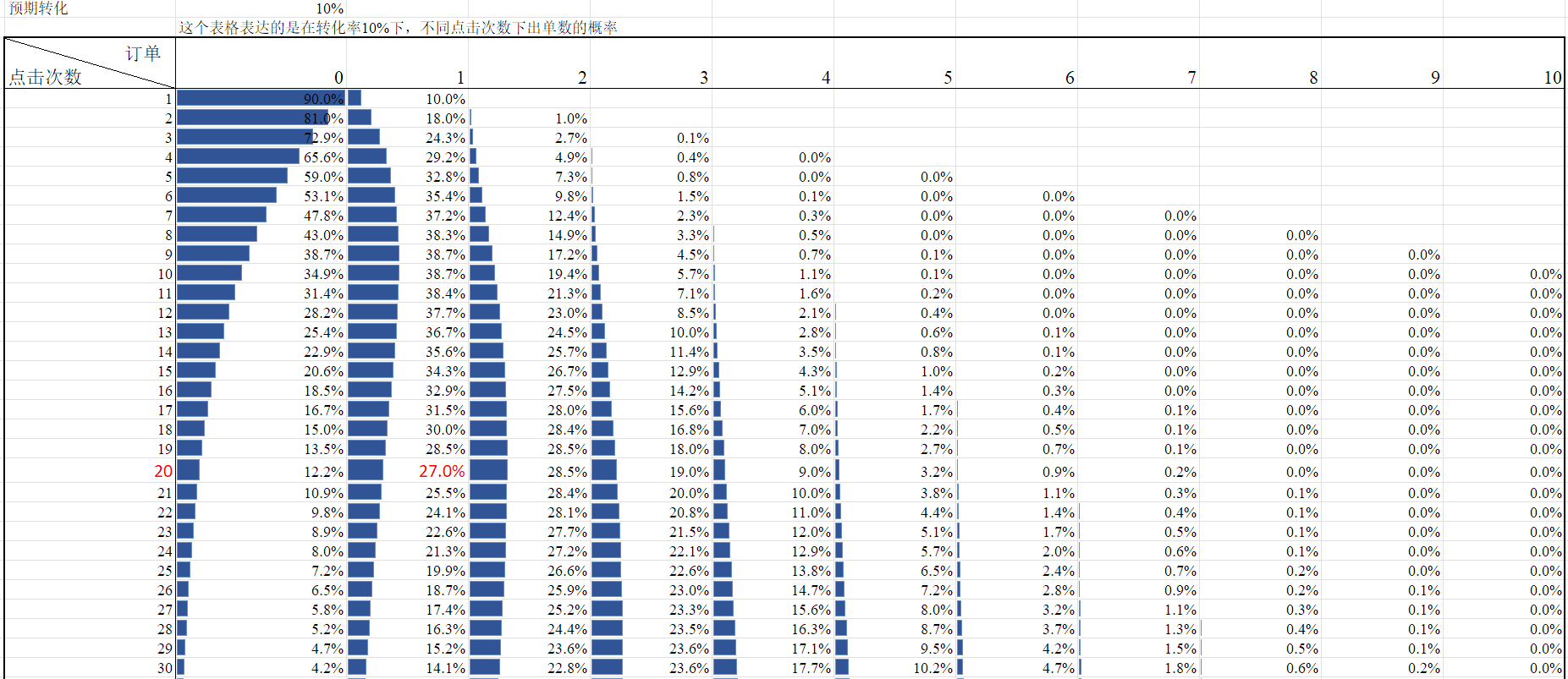
- 一个转化率10%的词究竟会在第几次出单?出单的概率多大?
上图可以回答这个问题
如果在某次点击后依旧没有出单,那么他为10%转化率的概率究竟还有多大?
EXCEL可以利用以下算法实现假设检验的概率计算
1
=(IFERROR(BINOM.DIST(C$7,$B9,$C$5,FALSE),"")
这里需要的就是假设检验,即假设转化率为10%的情况下,某个点击次数下,订单为具体数值的概率为多大。
EXCEL可以利用以下算法实现假设检验的概率计算
1
2
3
4
5
6
7
8
9
10
11
12
13=IF(
(
1-IF(
C7<=ROUNDUP(B7*$C$1,0),
BINOM.DIST.RANGE(B7,$C$1,C7,ROUNDUP(B7*$C$1,0)),
BINOM.DIST.RANGE(B7,$C$1,C7)))<0.5,
BINOM.DIST.RANGE(B7,$C$1,0,C7),
1-IF(
C7<=ROUNDUP(B7*$C$1,0),
BINOM.DIST.RANGE(B7,$C$1,C7,ROUNDUP(B7*$C$1,0)),
BINOM.DIST.RANGE(B7,$C$1,C7)
)
)
1.3.4延申思考
由于概率分布的特性,现实中我们应该关注广告的累计转化率,而不是具体的某个时间点的分布,因为点击数较小的情况下,你求出来的转化率未必是产品的真实转化率。
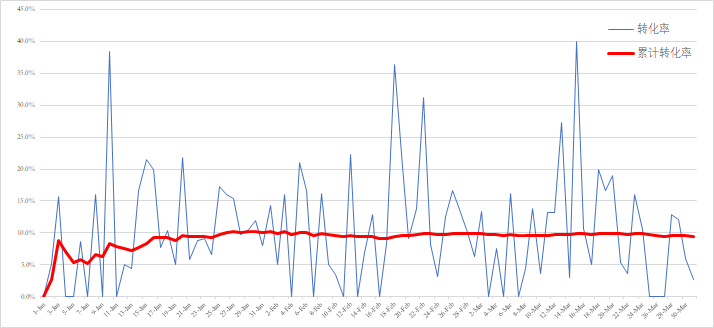

在累计转化率相同的情况下,通过多次数据模拟也可以发现不一样的累计转化率走向,如果不理解这个道理,很容对表现相同的产品做出完全不同的方案。
1.4 莱温斯特编辑距离和关键词相关性判断基础知识
莱文斯坦距离,又称Levenshtein距离,是编辑距离(edit distance)的一种。是描述由一个字串转化成另一个字串最少的编辑操作次数,其中的操作包括插入、删除和替换。
举例:
- 例如将kitten一字转成sitting:
- sitten(k替换为→s)
- sittin (e替换为→i)
- sitting (添加→g)
- 那么二者的编辑距离为3。
通过和字符串长度建立相对距离,可以帮助我们判断相似性
1.4.1 实际应用
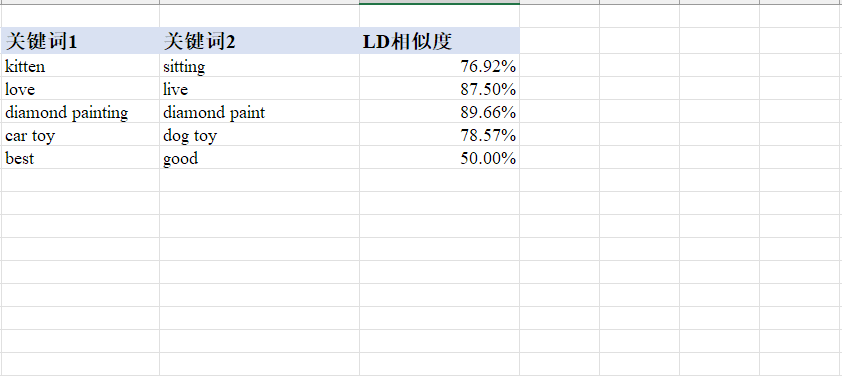
1 | Function Levenshtein3(ByVal string1 As String, ByVal string2 As String) As Long |
1.4.2 延申探讨
常见的语义的相似度分析
- Word co-occurrence methods
- Similarity based on a lexical database
- Method based on web search engine results
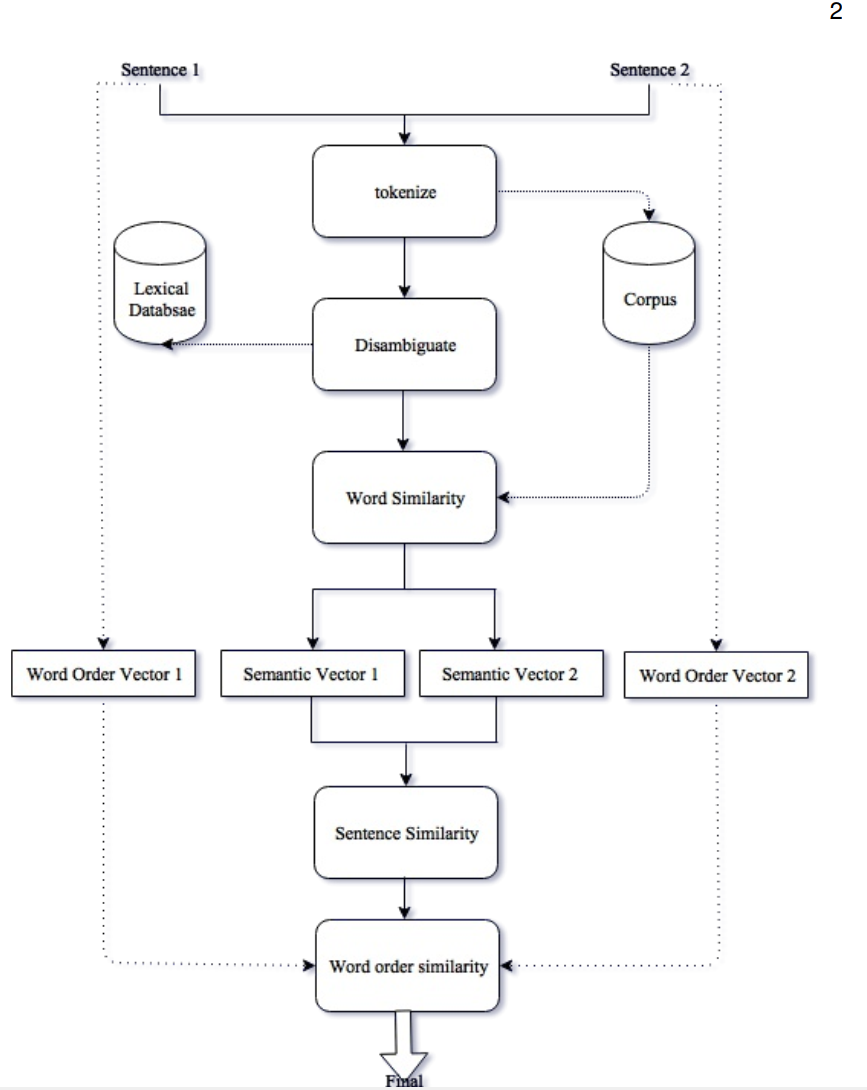
不想写了